纸莎草⽣⻓在尼罗河三⻆洲中,采摘后,⼈们将其茎杆中⼼的髓切成细⻓的狭条,压成⼀⽚,经过⼲燥处理,形成薄⽽平滑的书写表⾯。古埃及⼈⼀直在这种纸上书写,后来也被希腊⼈、罗⻢⼈使⽤, 直到3世纪才被价格更低、可以两⾯书写的⽺⽪纸(源于⼟⽿其)取代,但埃及⼈⼀直 使⽤到8世纪。

纸莎草

莱茵德纸草书
这部纸草书总⻓525厘⽶,⾼33厘⽶,最初应该⾮法盗掘于底⽐斯的拉美西斯神庙附近。1858年为苏格兰收藏家莱因德购得,现藏⼤英博物馆。纸草书的内容分两部分,前⾯是⼀个分数表,后⾯是84个 数学问题和⼀段⽆法理解的话(也称为问题85)。问题涉及素数、合数和完全数,算术,⼏何,调和平均数以及简单筛法等概念,其中还有对π的简单计算,所得值为3.1605。 莱茵德纸草书,⼜被称为阿姆⼠纸草书,以纪念公元前1650年左右⼀位抄录此书的书记官。 莫斯科纸草书,成书⼤约在公元前1850年。该⽂件⾥已经有锥体体积公式,很了不起的成就,难怪古埃及可以造出建筑史奇迹⸺⾦字塔。
⼀道例题:

从这个⽂件⾥,可以看到,古埃及已经能较熟练地运⽤分数了,事实上古埃及分数是数论研究⾥的重要课题。
古埃及⼈将荷鲁斯之眼(真知之眼)拆解为6个部分,每个部分各代表着⼀个单位分数,构成⼀个等⽐级数,相加起来便是⼀个荷鲁斯之眼,代表着1。
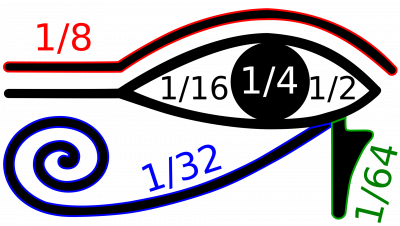

古埃及的分数是不同的单位分数的和,就是分⼦为1,分⺟为各不相同的正整数。 任何正有理数都能表达成这⼀个形式。例如:3/4可以写成1/2+1/4,⽽2/5可以写成1/4+1/10+1/20。
试⼀试、想⼀想:
- 1/3=1/a+1/b,求a和b,a、b都是正整数;
- 想把5个饼⼲平分给6个⼩孩,但是,每个饼⼲都不能分成6等分。
- 5张纸,每张都不能分为8等分,⽽平分给8个学⽣的⽅法是什么?