作者|徐利治
来源 | 《数学通报》,2000年第5期

我出生在长江之滨,很喜欢苏轼的诗句:“哀吾生之须臾,羡长江之无穷。”看来这诗句隐含有劝人珍惜年华、努力向上之意。
我们知道,在正常情况下,一般从事数学职业者在人世间还算是比较长寿的。例如从数学史书上可以看到,19世纪至20世纪的众多数学家的平均寿命都在“古稀年龄”之上。迄至2000年,我也将有55年的数学教学工龄了。所以这篇谈话,真可说是“老生漫谈”了。
积半个世纪的数学教学与科研工作经历,我的个人经验可概括为五句话:一是培养兴趣,二是追求简易,三是重视直观,四是学会抽象,五是不怕计算。
最后要说的是,数十年来,使我真正体验到了两条客观规律,即“兴趣与能力的同步发展规律”和“教、学、研互相促进的规律”。我认为这些规律理应成为现代认知心理学和科学方法论中值得探讨的规律。
下面就让我来谈谈个人的一些经验与体会。
1、培养兴趣
我把培养兴趣置于首要地位,因为众所周知,兴趣有助于集中注意、活跃思想,并能助长克服困难的勇气和毅力。要想有成效地学习和研究数学,尤其非要有兴趣不可。
记得我上初级小学时,对算术一点兴趣也没有,速算测试成绩也较差。到了高小阶段,有一阵忽然对“鸡兔同笼”等问题产生了好奇心。有一天我伯父把听来的一个“怪题”拿来考我:“100个和尚分100个馒头,大和尚1人分3个,小和尚3人分1个。问有多少个大和尚和小和尚?”我利用学到了的鸡兔同笼问题的推理方式,居然得出了有25个大和尚与75个小和尚的正确答案,伯父很是赞许。自此以后,我就特别喜欢求解算术应用题,开始学到了用算式表达事物间简单数量关系的能力。这种能力其实也可以看作是最低层次的“数学建模能力”。
后来我读了师范学校,买到一本陈文翻译的《查理斯密大代数学》;对书中的级数与连分式、排列与组合、或然率论、初等数论和方程式论最感兴趣。还作了一些难题和怪题,很觉高兴而自豪。与此同时我还津津有味地读了一本引人入胜的《算学的故事》(章克标著,开明书局出版)。就这样,我就开始热爱起数学来了。但当年丝毫也不敢设想成年后能靠搞数学来吃饭。直到后来有机会进了西南联合大学,才把尔后搞数学职业选择成为自己的人生道路。
上述的个人经历,使我明确地认识到,兴趣和才能是互相促进的。而兴趣的培养和发展,其最有效的途径就是要多读一些富于启发性的数学史书和数学家故事,还要经常保持做些有趣题目的习惯。我认为成功的数学教师,应该经常能向他或她的学生们讲讲数学家的有趣故事,还要能做到像乔治·波利亚(G. Polya)所主张的,“好的数学教师要保持做题的好胃口。”
我想,时至今日谁也不会主张在小学和中学里多搞些难题和怪题,特别不应把难题怪题用作考试题目。但是为了激发青少年的好奇心和兴趣,也为了帮助他们增长智慧和才能,在教学中有选择地采用少量有趣怪题(例如著名的“鸡兔同笼”问题等)也是未尝不可的。
2、追求简易
1948年我在清华大学做助教时期,有一次听完陈省身先生的讲演后,记得他曾向我们几位青年教师介绍了欧洲一位数学大师的一句名言:“数学以简易性为目标” (Mathematics is for simplicity)。当年我对这句名言体会不深,主要是对“简易”这个词的真实涵义理解不透。
那时候我讲授初等微积分课程,逐渐领悟到作为微积分核心基石的“微积分基本定理”——牛顿--莱布尼兹公式——在原理上是十分简明的,在方法上又是易于操作的。这样既简明又易于操作的公式,不正是表明“简易性”的特征吗?
后来我又读了一些有关“微积分发明史”的资料,得知17世纪60年代前,人们为了处理各种各样的无穷小量求和问题,曾走过了漫长而艰辛的道路。而牛顿--莱布尼兹公式的提出,才把许多复杂艰难问题的求解过程,统一于一条简易的基本定理。这也说明,微积分的创立正是以“简易性”目标的实现为标志。
有位朋友告诉我,中国古代的《易经》上已对”简易”一词作了很好的解释:“简则易知,易则易从”。意思是说,简单的原理易于明白,容易操作的东西便于应用。事实上,数学上许多有价值的理论和方法以及重要的定理与公式,基本上都是具有简易性的科学成果,而简易性或者简单性也是数学美的特征。
在我长期的数学工作实践中,我总是不忘记对简易性成果的追求。一般说来,我感兴趣的问题,我总是希望努力把它简化到不能再简单的程度。然后对简化了的问题再努力寻找其简易解答。这些努力未必总是成功。如果失败了,则凭着我对问题的浓厚兴趣,我还将另觅小路,继续前进。在我指导青年学生作科学研究时,我也总是强调,首先要学会化难为易、化繁为简的本事,当他们取得了简易性的数学结果,如果真是优美而有用,我就会以“漂亮成果”一词作为赞许。
对待数学教学,包括编教材和讲课,我也一贯喜欢以追求“简易”为目标。这一点,多半是受了我大学时代老师华罗庚先生的影响。记得在我大学中业后担任华先生助教时期,他曾告诉我下述观点:“高水平的教师就能把复杂的东西讲简单,把难的东西讲容易。反之,如果把简单的东西讲复杂了,把容易的东西讲难了,那就是低水平的表现。”有时候,我也曾听说过有些数学教师为了在学生面前卖弄学问,故意把容易的东西讲难了,把简单的东西讲复杂了。
上述华罗庚先生的教学法观点实际是和乔治·波利亚的数学思想不约而同的。我个人认为,今后全国大、中、小数学教学的改革事项中,无论是教材内容改革或教学方法改革,应和数学发展的总的目标要求相一致,即必须以“追求简易”为目标。
3、重视直观
无论是从事数学教学或研究,我是喜欢直观的。学习一条数学定理及其证明,只有当我能把定理的直观含义和证法的直观思路弄明白了,我才认为真正懂了。例如,当年我以好奇的心情学习维尔斯特拉斯(Weierstrass)著名的连续而处处不可微的函数时,经过一阵耐心的精微的思考之后,我才真正弄明白了函数结构设计的直观背景和证法的基本思路。由此类似思路,不难构造出任意多的具有不同形式的连续不可微函数例子。
在科学研究中,我也常常借助于由经验获得的直观能力。以猜测的方式去探索某些可能取得的成果。当然,失败的经验也是很多的。这里我乐于谈一个我取得成功的例子。
1964年我吉林大学任教期间,一度对超越方程求实根问题发生了兴趣。研究目标是希望能找到无估算初值的“整体收敛迭代法”。我们知道,求解高次代数方程的实根已有这种性能的迭代法,即著名的拉盖耳(Laguerre)迭代过程。
我联想到欧拉(Euler)在寻求著名的级数和
\sum_{n=1}\frac{1}{n^2}
时,曾经把正弦函数的幂级数展开式大胆地看成为无限次多项式,从而通过类比法得到了正弦函数的因式分解的无穷乘积公式。最后他把乘积展开后与幂级数二次幂比较系数,便成功地解决雅谷·柏努利(Bernuoulli)的级数求和难题。即求得了级数之和。
\sum_{n=1}\frac{1}{n^2}
欧拉的思想方法给我的重要启示是,一定条件下,幂级数可以看作是次数为无穷大的代数多项式。这使我联想到拉盖耳迭代公式中的参数n(即所论代数方程的次数)应能令它趋向于∞而获得适用于超越方程的迭代方法。再由观察立即看出 n→∞ 时拉氏公式仍继续保持合理意义,而且形式更简化了。这样,我便猜到了一个可以用来求解超越方程的大范围收敛迭代法。最后,应用整函数论里的阿达玛(Hadamard)因式定理,果然证明了上述方法的大范围收敛性。(此项结果发表于1973年美国数学会通讯摘要栏)。
上述研究给予我的深刻印象是,由类比联想引发的直观与猜想有时真能成为发现新成果的源泉。因此,在以往20多年里我始终热心地提倡数学工作者和数学教师们,值得花足够的时间去研读乔治·波利亚的两本名著,即《数学与猜想》与《数学的发现》。
一般英文辞典中,常把intuition译作直觉、直观,足见直观与直觉两词的涵义会有不少相通或相同之处。但在数学中,我宁愿把“直观”一词解释为借助于经验、观察、测试或类比联想,所产生的对事物关系直接的感知与认识。例如,借助于见到的或想到的几何图形的形象关系产生对数量关系的直接感知,即可称之为“几何直观”。我在本文中要强调的观点是,有作为的数学工作者与教师都应重视数学直观能力的培养与训练。
4、学会抽象
我们知道,许多现代数学家都倾向于承认数学是研究模式的科学。关于模式的原始观念可追溯到古代的柏拉图。我们个人也相信数学是以理想的量化模式作为研究对象的。这里,所谓的量化模式或称为数学模式,是泛指反映事物关系(包括空间形式与数量关系)的纯粹形式结构。这种纯粹形式结构必须是科学抽象的产物。所以理应具有概念上的精确性,简易性,逻辑可演绎性与普适性。例如,自然数1,2,3,…是反映了离散事物顺序计数的数学模式。微积分学是反映变量计算规律的一个大型数学模式。当然,数学中的每一条公理,定理,公式,典型的计算方法或者程序,以至于成型的推理法则(如数学归纳法,超穷归纳法以及康托尔--希尔伯特对角线论证法等),也都是或大或小的数学模式。
前面第二节,我们已谈论到数学是以追求简易性为目标的。可是数学模式的简易性要求正是由概念方法上的统一性与概括性(普遍性)来体现的,而这又必须通过抽象过程来实现。换句话说,抽象是达到数学模式简易性目标的必要手段和过程。因此,时刻要与数学模式打交道的数学工作者与青年教师都有必要及早领会和学会数学抽象的方法及技巧。
其实,只要仔细考察分析数学上一些较典型的抽象定理和它们众多的具体特例,都会发现它们是从特殊到一般、从具体到袖象的产物。我自己就是遵循这样一条观察分析的学习途径去获得数学抽象的基本技能的。
一般说来,数学抽象包含有四个步骤,即(1)观察实例,(2)抓住共性,(3)提出概念,(4)构筑系统或框架(理论)。下面作为解释四个步骤的例证,我就来谈谈当年我是如何想到去提出“关系(Relation)映射(Mapping)反演(Inversion)原则”的。这原则也是一种普遍方法,可简称为RMI原则或RMI方法。最近十多年来,看来国内研究方法论的学者的一些论著中,都已认可和使用了这一名称。
那是在1980年左右,我曾在国内三所大学讲授过“数学方法论”,很喜欢向学生们介绍“哥尼斯堡七桥问题”、“斐波那契数列计算问题”、“拉普拉斯变换求解微分方程”等问题的思想方法。在准备讲稿时,我很自然地意识到这些问题虽然形貌各异,但解决问题的核心思想却是相同的。即都是利用了某些(包括广义的)映射与逆变换概念。进一步的联想,还使我想到了诸如初等数学中的对数方法,解析几何方法,概率论中的特征函数方法,组合分析中的生成函数方法,偏微分方程论中的狄利克雷原理,甚至庞卡莱与克莱因在欧氏平面上构筑非欧几何模型的思想方法。本质上也都是各种映射(变换)与反演(逆变换)方法的具体实现。
正是对上述诸实例的共性有了全面的了解,才使我能够使用数学语言来表述如下一系列普遍概念:关系结构(R),未知原象(x),映象结构(R),未知映象(x),可逆可定映映射(φ),定映方法(Ψ),已知映象(x*),反演(φ-1)。于是作为普遍解题模式的RMI方法即可表述成如下程序:
这里的x*,x即表示通过与Ψ与φ-1两个步骤所求得的映象与原象(即问题(R,x)所要求的解答)。
当然上面提到的各个著名问题与重要方法都属于上述一般RMI方法的特例。例如,在解常微分方程初值问题的拉氏变换法中,常系数微分方程与初值条件形成关系结构R,而x便是要求的解函数。作为映射工具的φ是拉氏变换,φ-1便是逆变换。在拉氏变换下映象结构R往往成为代数方程组,于是通过代数方法将解x求得后,再对x*施行逆变换φ-1便求得解函数。
又例如在哥德尼斯堡七桥问题中,桥与岛及陆地的连接关系作成关系结构R,而能否一次通过七条桥的问题成为未知原象x。欧拉将桥抽象成为线,将岛与陆地抽象成为点,从而R变为点线图R,这一过程可称为“概念映射”φ。在这—映时下,七桥问题(R,x)即变换成一笔画问题(R,x)。于是通过一笔画交点特征分析法Ψ,得知一笔画问题之不可能性的答案x。由于φ具有逆映射φ-1(即可由抽象返回具体),故结论便是一次通过七桥是不可能的(此即答案x)。
一般说来,凡能使用有限多次RMI方法就可获得解答的数学问题即称为“RMI可解问题”,而所需次数称为可解问题的“阶数”。
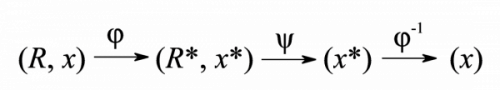
在1983年出版的拙著《数学方法论选讲》一书中有专章论述RMI方法并有一批应用实例,感兴趣的读者可以查阅(该书第三版已在2000年问世)。非常巧合的是,同在1983年美国数学史专家H. Eves在他出版的《数学的伟大旅程碑》(the Great Moments of Mathematics)书中,也在一章描述了RMI思想方法。但该章主题是论述解析几何发明史,而未将RMI抽象成为普遍的方法论原则。当然,Eves的著作是很富于见解的。
上面借助于例证说明了“从特殊到一般”的—般性抽象方法。事实上,在数学研究中,有时为了深化数学研究内,扩大数学应用应用领域,还常常要在—般性的数学结构上,利用引入新特征(新概念)的办法去得到更有深刻而丰富内涵的新结构或新对象。这种“从一般到特殊”的概念深化过程称之为“强抽象“。
例如,在连续函数类上引进“可微性”概念便得到了可微函数类。显然后者在结构上比前者更特殊化了。但如果没有这种抽象特殊化,又怎能产生微积分学呢?又如果不在—般的巴拿赫(Banach)空间上引进“内积”概念从而导入更有深刻内涵的希尔伯特(Hilbert)空间概念,那又怎能使泛函分析成为现代物理科学中的重要工具呢?数学上有许多著名例子使我们认识到,强抽象是理论研究中最富有成果的数学抽象过程。所以我认为数学工作者理应持别重视“强抽象”。
强抽象的关键是把—些表面上不相关的概念联系起来,设法在其中引进某种关系或“运算”,并把新出现的性质作为特征规定下来,从而构造出新的数学结构成模式。这种抽象法则可称为“关系定性特征化法则”,凡是精通这—法则而又有深厚具体应用背景知识的数学家,往往能由此作出创造性的贡献来。因此我认为,凡希望对数学做出创新成果的青年数学工作者,应努力学会正确地运用“关系定性特征化法则”去构筑有价值的数学新结构或新模式。
5、不怕计算
不怕计算可以说是我在长期数学工作中养成的一种性格或习惯。我在小时候是不喜欢做算术计算题的,甚至对复杂的计算很害怕。后来,学了中学代数和三角学,学会把复杂的式子化成最简式,感到是一种愉快。有时看到或得到一些很有规律的对称式,很觉得高兴。
我相信,人人都有爱美之心。而数学结构形式(包括公式与各种关系)间的简单性、规律性与对称性等正好是美的特征,所以我之开始喜欢计算并学会计算,大概与我喜爱“数学美“的天性有关。
在以往的数十年里,我从事计算数学的方法与理论研究,更是时时与分析计算打交道。这样,我就培养了对计算的兴趣与耐心。特别我很喜欢从复杂的计算过程中寻找规律,寻觅最简洁的结果。有时候意想不到的简单结果会带给我极大乐趣。
例如,60年代我自己最感兴趣的一个工作是,我发现在最一般形式的“快速振荡函数积分”的渐近展式中,居然出现重要的积分因子——伯努利多项式。这一结果是通过一系列计算后发现的。包含这一结果的文章发表发表于1963年[见英国Pro. Cambridge Phil. Soc., 59:1(1963)]。说来奇怪,时过24年后,美国三位学者的合作论文中又重新发表了我的结果的特例[见美国Math. Comp., 49(1987), 作者为V. Banerjee, I. Lardy, A. Lutoborski].
计算能帮助发现规律,发现漂亮的新结果,这些正是推动人们能耐心地从事复杂计算的心理动力。所以根据我个人的学习与工作经验,我赞成应利用青少年的爱美的天性和寻求新结果的好奇心,配以启发性的教材,让他们不怕计算,学会计算,并能从计算中寻找乐趣。
尾声
最后,我想谈的是,我一生中的绝大部分数学知识实际是通过自学和教学工作过程获得的。我在大学毕业时,连什么是勒贝格积分,调和分析研究些什么,什么叫做巴拿赫空间,什么是群论中的伽罗瓦(Galois)基本定理,如此等等均一无所知。后来,由于教学需要,我曾先后讲授过十七门数学课程,通过自学与教学才逐步弄明白了许多数学分支的重要题材,甚至有些靠自学得来的知识还成为我写作论文的基础。因此,在我长期的数学生涯中,我深切体会到“教、学、研相互促进的规律”。在这里我乐意将这条规律——指导我成长的一点经验——介绍给我国的年青数学工作者。
作者简介: 徐利治(1920年9月23日—2019年3月11日),出生于江苏省张家港市,1945年毕业于西南联合大学,1946年加入中国共产党。中国数学家、教育家,大连理工大学教授。致力于分析数学领域的研究,在多维渐近积分,无界函数逼近以及高维边界型求积法等方面获众多成果,并在我国倡导数学方法论的研究。