弗拉基米尔·阿诺德（英文 Vladimir Igorevich Arnold，19372010.6.3），20世纪最伟大的数学家之一，动力系统和古典力学等方面的大师。
阿诺德开创了几个数学领域，如几何力学、辛拓扑及拓扑流体动力学。《世界报》援引俄罗斯科学院副院长的话说，“弗拉基米尔·阿诺德是当代最杰出的数学家之一，他的工作为其他科学研究做出了不可忽视的贡献。”
阿诺德对数学教育也很有见解。他的教科书以及他的学生也对数学界产生了深刻的影响。他的名著 《Mathematical Methods of Classical Mechanics》 是公认的经典教科书。
但不很为人所知的是，阿诺德曾被认为是问题儿童，启发他的天赋的是一位好的老师及其问题。老师提出的数学问题是：从两镇同时出发相向而行的两位老妪，在中午相遇，再继续走向对方小镇，分别于下午四点和晚上九点到达目的地，问她们是何时起步的？当然此题代数求解非常容易，但那时他们还未学到代数。阿诺德用了相似性的理由发明了“算术”解，体验了发现的快乐。
阿诺德认为，想要再次体验这种快乐的欲望，才是使他成为数学家的要素。
同时，阿诺德深信，传统俄罗斯的思维发展训练最早是通过独立思考简单但不容易的问题来培养的。
2004年春，一些在巴黎居住的俄罗斯人请阿诺德帮助他们的年轻孩子进行这样的训练，最后的成果就是阿诺德的书《讲义和问题：给青年数学家的礼物》。
下面的30道题出自《讲义和问题：给青年数学家的礼物》一书，以飨读者:
玛莎（Masha）身上的钱买一本字母书差7戈比，美莎（Misha）身上的钱买这本书差1戈比。她们把身上的钱合起来买这本书还是不够。问这本字母书多少钱？（译者注：戈比是俄罗斯最小的货币单位）
一个带有软木塞的瓶子售价为1.1美元，而瓶子本身比软木塞高出10美分。问软木塞值多少钱？
一块砖的重量是一磅加半块砖的重量。问这块砖重多少磅？
从一桶葡萄酒中取出一勺葡萄酒放入一杯茶（未满）里。之后，将等量的一勺玻璃杯混合液体倒入葡萄酒桶中。此时，每个容器里都有一定量的“外来”液体（玻璃杯里的酒和桶里的茶）。问哪一种外来液体的体积更大：桶里的茶还是玻璃杯中的酒？
两名老年妇女在黎明时离开，一名从A到B，另一名从B到A. 她们（沿着同一条路）相向而行。她们在中午见面，但并没有停下来，并且她们每个人都以以前一样的速度继续前行。第一位女士在下午4点抵达B，第二位女士晚上9点抵达A。问她们是当天黎明几点出发的？
6.（在一个美国标准的测验中）一个直角三角形的斜边是10英寸，此斜边上的高是6英寸。求此直角三角形的面积。
维克多 (Victor) 的姐妹比他的兄弟多2个。问维克多的父母的女儿比儿子多几个？
南美洲有一个圆形的湖泊。每年的6月1日，一朵王莲花 (Victoria Regia flower) 出现在它的中心。（它的茎从湖底部升起，它的花瓣像睡莲一样躺在水面上）。每天花的面积加倍，至7月1日，它终于覆盖整个湖泊，然后花瓣落下，其种子下沉。问几月几号时，花的面积是湖泊面积的一半？
一个农夫必须把一只狼，一只山羊和一棵白菜运过河。但是这艘船太小了，他每次只能带这三个中的一个过河。问他怎样才能把这三个都运过河去？（狼不能和山羊单独呆在一起，山羊不能和白菜单独呆在一起。）
白天，蜗牛在一根柱子上向上爬了3厘米。在夜间，它睡着了，向下滑了2厘米。这根柱子有10米高，一个美味的甜点正在柱子顶端等待蜗牛。问蜗牛要花多少天才能品尝到甜点？
一个猎人离开他的帐篷向南走了10公里，然后向东直行，走了10公里，射杀了一头熊，然后转身向北走了10公里后发现了自己的帐篷。问熊是什么颜色？这是在哪里发生的？
今天中午十二时发生满潮。（在同一地点）满潮明天几点发生？
两卷普希金的书，第一卷和第二卷，并排放在书架上。每卷书的页面总厚度（不包含封面和封底）为2厘米，封面和封底各有2毫米厚。书虫从第一卷第一页啃到第二卷的最后一页（垂直于页面啃咬）。问书虫的轨迹有多长？[ 这个拓扑问题有个令人难以置信的答案 — 4mm — 这对于院士来说是完全不可能的，但是一些学龄前儿童可以轻松应对。]
作者注：在提出这个问题的时候，我试图在2000年“物理学进展”杂志百周年期刊的邀请论文中说明数学家和物理学家在研究方法上的差异。我的成功远远超过了我所想到的目标：我的设计是基于学龄前儿童的经验，与编辑们的经验不同，所以编辑们不能解决这个问题。所以他们为了得到答案4毫米把题目改成了下面的方式：他们改成了“从第一卷的最后一页到第二卷的第一页”，而不是“从第一卷的第一页到第二卷的最后一页”。
这个真实的故事是如此令人难以置信，所以我要把这个题目写进来：证据是杂志发表的编辑版本。
- 从上面和从前面看，某个物体（多面体）的形状如下。画出从侧面看它的形状。（多面体的隐藏边用虚线显示。）
俯视
前视
有多少种方法将数字64分成十个自然数之和，其中每个自然数不超过12？只有加数顺序不同的和不能算作不同的和。
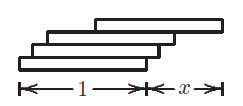
我们有一些质地相同的块（比如，多米诺骨牌）。我们把这些块堆放起来，使得最上面的块比最底下的块移出x长度。问：x最大可能是多少？
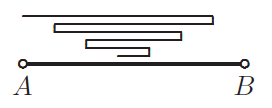
- A镇和B镇之间的距离是40公里。两名骑自行车的人从A和B同时离开相向而行，一个以10 km / h的速度行驶，另一个以15 km / h的速度行驶。一只苍蝇与第一个骑手一起离开A，以100公里/小时的速度飞向第二个骑手。苍蝇遇到第二个骑手时，触碰到他的额头，然后飞回到第一个骑手，碰到他的额头，再返回到第二个骑手，一直这样下去，直到两个骑手的额头碰撞并压扁苍蝇。问：苍蝇一共飞行了多少公里呢？
- 瓦尼亚（Vanya）解决了一个关于两个学龄前（preschool）儿童的问题。在给定两个孩子年龄乘积的情况下，瓦尼亚必须找出他们的年龄（这是整数）。
瓦尼亚说这个问题不能解决。老师称赞他说得对，然后给这个了问题增加了条件：大孩子的名字是佩蒂娅（Petya）。这时瓦尼亚可以马上解决这个问题。现在请你解答这个题。（译者注：美国的学龄前（preschool）指的是不超过5岁的孩子。）
整数140 359 156 002 848是否能被整数 4 206 377 084 整除？
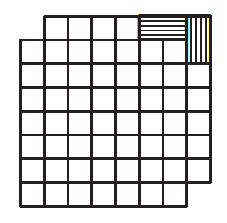
一块多米诺骨牌可以覆盖棋盘的两个方格。请用31块多米诺骨牌盖满一个除去左上和右下方格（在同一对角线上）的棋盘。（一个棋盘由8×8 = 64个方格组成）
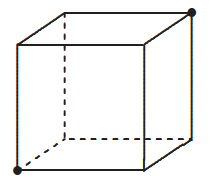
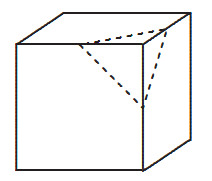
- 一只毛毛虫想要从一个立方体房间的地板的左前角爬到另一个角落（天花板的右后角）。请找出沿着房间墙壁的最短路线。
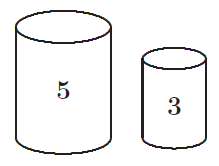
- 你有两个容器：分别为5升和3升。用它们测量出一升液体，并将液体留在其中一个容器中。
家里有五个脑袋和十四条腿。问家里有多少人，多少只狗？
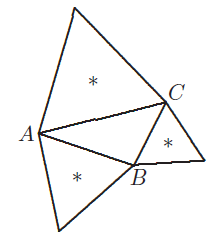
在三角形 ABC 的边 AB，BC 和CA的外部构造三个等边三角形。证明这些等边三角形的中心（在图上用星号标记）构成一个等边三角形。
- 用平面切割立方体得到的截面可能会是什么多边形？我们能得到五边形吗？七边形？正六边形吗？
画一条直线穿过一个立方体的中心，使得从立方体的八个顶点到它的距离的平方和为（a）最大，（b）最小（与其它这样的直线相比）。
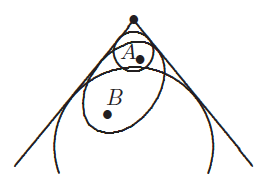
一个正圆锥体沿着一条闭合的曲线被一个平面切割。圆锥体的两个内切球与平面相切，一个在A点，另一个在B点。在横截面上找到一个点C，使距离CA + CB之和为（a）最大，（b）最小。
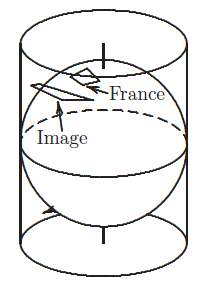
- 地球表面投射到一个圆柱体上，这个圆柱体由与经线相切的直线构成，这些直线与赤道的交点正是直线与经线的切点。这个投影是沿着平行于赤道平面的光线作出的，并通过连接地球的北极和南极的地球轴线。问：法国的投影面积是否大于或小于法国的面积呢？
证明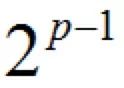
除奇素数p的余数为1.
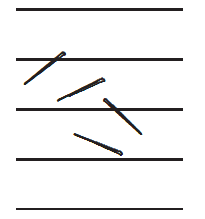
将一根10厘米长的针随机扔到格子纸上。纸上相邻线之间的距离也是10厘米。重复N（比如一百万）次。问：多少次（在百分之几的误差内）针会落下与纸上的一条线相交？
人们可以用N = 100而不是一百万次投掷来进行 这个实验。（我十岁的时候做过这个实验。）
这个问题的答案是令人惊讶的：(2/π)N. 而且，即使对于长度为a·10 cm的弯曲针，在N次投射中观察到的相交的次数也约为(2a/π)N. 由此得到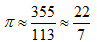 
收藏小程序，购书有优惠
如果您有购书需求，可以关注当当优惠券小程序，优惠券将会在第一时间发放在小程序中，敬请收藏。
