苏联学者加里宁说过:“数学是锻炼思维的体操”。 好的数学问题能锻炼思维、发展智力、扩大视野、提高能力,增加学习数学的兴趣。如果你能积极地投入,你会觉得数学并非是枯燥无味的,而会使你兴趣盎然。有人说过数学是一座大花园,会被其中的美沉迷而流连忘返。
下面我们提供几道饶有兴趣的问题来启发你的智力。首先你不妨自己先思考,能否有新颖而简洁的解法,实在想不出来,可以回复本主题查看答案。
1、不通过计算,求出两相似图形的面积比
图 1 中的大正方形面积是小正方形面积的几倍?
图 2 中大三角形的面积是小三角形面积的几倍?
请你不通过计算给出答案。
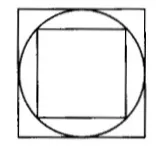
图 1
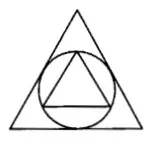
图 2
2、在逻辑排列中,图 3 图 4 的右下角应填什么图形?
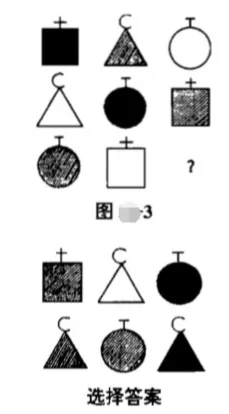
图 3
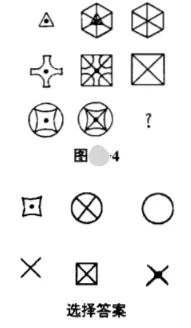
图 4
3、到底转了几圈?
如图 5、图 6,桌子上紧挨着放着两枚同样大小的硬币。它们外切于 A 点,C1 固定不动,C2 沿着 C1 币外缘无滑动地滚动,C2 币滚动一周后,C2 币与 C1 币又仍相切于 A 点。问 C2 币自转了几周?
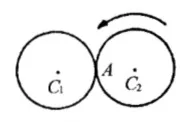
图5
图6
4、三用瓶塞
某人收集了三只瓶子,它们的瓶口形状分别如图 7 中的(a),(b),(c)。现在他想只做一只瓶塞,对三个瓶子都能适用,请你帮他设计一下。(未学过立体几何的读者不妨用切削萝卜来试试)
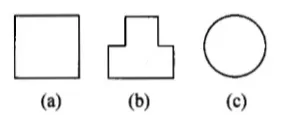
图 7
5、大小圆周一样长(亚里士多德诡辩)
如图 8 在轮子上有两个同心圆,轮子滚动了一周,大圆上的点 A 平移到了点 A’,小圆上的点 B 平移到了点 B’,显然 AA’=BB’,这不说明了大圆周长等于小圆周长吗?那么问题出在哪里?

图 8
6、曲线等分正三角形面积
用什么曲线将一个正三角形分为两面积相等的部分,并使曲线的长最短(如图 9)?
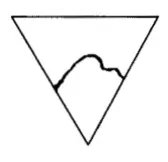
图 9
7、组合多面体有几个面
如图 10,“一个正三棱锥和一个正四棱锥,所有的棱长都相等,问重合一个面后的组合体共有多少个面?
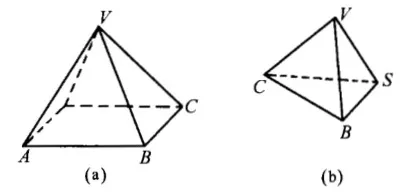
图 10
8.自鸣得意的学者解方程
某学者见到一道解方程的题,如图 11:
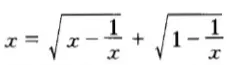
图 11
说道:“这还不容易,只需将这个方程脱了根号,变成一个四次方程去解,不就行了。”
聪明的读者,你能不解四次方程就作出这道题吗?
9.三等分圆面积
如果让你将一个圆的面积三等分,你很容易想到只需将以圆心为顶点的圆周角分成三个 120° 的圆心角,那么这三个角的边自然将圆面积三等分了。但如果有人问你,你最多有几种方法将圆面积三等分时,恐怕得要费一番脑子了!